You’re running a test on one of your landing pages with the primary goal of getting the user to click on a button. You are split testing (A/B testing) two different button colors (green and orange) to determine the impact of the button color on click-through rate. You collect the following initial results:
| Button Color | Visitors | Clicks | CTR (y) |
| Green | 38 | 2 | 5.2% |
| Orange | 39 | 3 | 7.7% |
The orange button is better, right?
Not necessarily. Sure, the orange button has a 7.7% click-through rate (CTR) compared to only 5.2% for the green button. However, the orange button has really only earned one more click. If the next visitor on the page clicks on the green button, both variants will have a 7.7% CTR, indicating that button color is irrelevant in this application.
Here is what happens if we run this experiment for several months with 16,000+ visitors:
| Button Color | Visitors | Clicks | CTR (y) |
| Green | 8,238 | 486 | 5.9% |
| Orange | 7,893 | 734 | 9.3% |
Is the orange button better now? Hell yeah, it is.
While the danger of making decisions based on too little data is an incorrect conclusion, the danger in collecting too much data is a waste of time, effort and money. Even though there was little data to determine orange was best in the first variant, had you decided to go with the orange button anyway, you could have sent all the above 16,000+ visitors to the page that performs at a 9.3% CTR. Thus, giving you a whole lot more sales/leads/etc.
So how many users are required to make this decision? We can use the following equation:
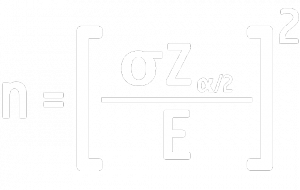
Where:
- n is the minimum sample size required to prove that the two variants are statistically different.
- Z is the z-value corresponding to the chosen confidence interval in the Table of the Standard Normal Distribution.
- E is typically known as the “error.” In this application, E is the difference between the mean values of two samples.
- σ is the standard deviation.
The Z-score that corresponds to 95% confidence is 1.64 (from the Table of the Standard Normal Distribution).
For example, let’s say you are using the data in the second table above, and you want to be 95% confident in your decision. E is the difference between the two sample means, so
E = 0.093 (orange CTR) – 0.059 (green CTR)
E = 0.034
To figure out the standard deviation, we can treat binary data like continuous data because of the Central Limit Theorem, which states that as a binary sample gets larger, its distribution approximates a continuous distribution. So, determine the overall CTR as follows:
total clicks = 486 + 734 = 1,220
Total visitors = 8,238 + 7,893 = 16,135
That means the overall conversion rate was
1,220 / 16,135 = 0.0756
In Excel, you can get the σ-value by using the function =NORM.S.INV(1-0.0756) which returns 1.435.
Putting all of that together, the equation to determine what minimum sample size is required to show an accurate, statistically significant improvement of CTR for the tested page with the orange button is:
n = ( (1.64*1.435) / 0.034 ) 2
n = 4791
Therefore. In this example you would need to make sure you have 4791 samples in order to prove that you have enough to make a statistically significant decision over which variant is better.
Most A/B testing software will take care of his for you. What you really need to understand about the equation is:
- As standard deviation increases (more variation in your conversion rate), you will need more samples.
- If you want more confidence (95% versus 90%), you will need more samples.
- As the difference in performance between the two variants becomes smaller, you will need more samples (it takes more data to make sure the difference isn’t just statistical noise).
Easy right? Now get to work.


Great post. I love that you’re actually getting to the math behind these statistical analysis algorithms we let run our marketing.
That said, I think it’s helpful to consider the time frame of the test (in addition to the sample size).
Several months is a long time to run a click-rate test. The longer you run a test, the more variables come into play that you have no control over (like real world events). And these variables will tend to change over time, further skewing results. A test run over the course of the next 3 months may have very different results than those run the months following that.
I guess I’m just saying: Gotta keep testing! :)
If I understand correctly, you’re saying to start the test, get some results (so you can compare sample variance), and then run the formula to see how many more conversions you need before you declare your results significant.
Seems like this methodology would leave you falling prey to “repeated significance testing errors”, as explained here: http://www.evanmiller.org/how-not-to-run-an-ab-test.html.
The advice he gives in that article is to set your sample size before you start your test. Because if you just keep coming back to check on it, you will be skewing towards false positives in significance. Curious about your thoughts on that.
Bob – That was a good article you linked to. I agree that you should have an idea of your sample size before you start, however, even to come up with a rough ballpark estimate, you would want to use the formula to make sure your predetermined sample quantity is enough to demonstrate significant results.
You can’t begin to determine the required sample size without knowing the standard deviation of the data you are measuring. Without knowing this, you won’t know whether the data from the test variant is really different or just noise. You can use the page’s historical performance as a baseline.
For the error (the difference between the baseline and the test measurement), you would want to use the difference between your baseline and your target output. The larger the difference you expect, the fewer samples you should need because a big change should stand out from the noise (which depends on the standard deviation).
Hey Scott,
Thanks for taking the time to write this up. I’m a bit confused though, you say that ( (1.64*1.435) / 0.034 )^2 ~= 37, but I’m getting ~ 4791 [1.64 * 1.435 = 2.3534; 2.3534 / 0.034 = 69.2; 69.2^2 ~= 4791]
Is there some other step you’re taking I’m not aware of?
You’re right, Jared. I just re-calculated and got the same thing. The post has been updated to reflect to new solution. Thanks for the feedback!
No worries! I was just confused why my results looked so different than yours. Thanks for updating!
Thanks for this great post Scott! It provides exactly what I was looking for. Just one clarification for me if you could please: The final answer 4,791 is the number of samples of the orange or the number of samples of the green and orange combined? Thanks so much!
Scott, scratch the question above. I’m pretty sure the 4,791 is the sample size of the orange. Another question though: I’m running a test and for the control I have 5,738 visitors with 162 clicks (2.8%) and for the test I have 5,682 visitors with 183 clicks (3.2%). Thus far the different between control and test is not statistically significant. Using your formula I get a sample size of 600K in order to get statistical significance. Is there another formula that I could use that would tell me when to stop the test, irrespective of statistical significance or not? There is always the chance that I might be up to 600K visitors for the test and still not have statistical significance. Thanks again.
Correct, the closer together the two results are, the more samples are going to be required to say that test is really better than control. This is because these aren’t just two data points, they are means that each have a standard deviation associated with them. So the problem is, when the means are close together and there is significant data in each data set, it is difficult to tell the difference between a statistically high, but normal, value from the control group and a statistically low, but normal, value from the test group. In a scenario like this, control and test are statistically no different.
My advice would be to alter the test to either generate a larger difference in the means or reduce variation. Either of these will diminish the number of samples required to produce a statistically significant result.
Great article!
I wonder how to find statistical significance in case of conversion rate(many per click). The total conversions that one click associates may be totally different every time. Is the statistical significance of conversion(one per click) enough to draw conclusion for the corresponding many per click too?
You can use the same formula for conversion rate (many per click). The conversion rates of your samples would be expressed as decimals and would have a mean value and standard deviation like any other numeric data.
Thanks for the reply Scott!
Yes, as you said, there is no problem in implementing the formula.
But, say that button A displays 20 products (max 20 conversions) and button B displays only 2 products (max 2 conversions). Say that, from the above calculation, I gathered required data and got result that button B yielded more conversions. But one can easily argue that the result is not because button B was attractive, but just because it contains more product (May be this condition contradicts the idea of A/B test). But I am trying to find out a method to show statistical significance in such a case that the two buttons lead to different number of products.
I would probably choose a different metric like total revenue that would be a better apples-to-apples comparison.
Scott,
I follow you through the whole methodology, but I cannot understand if the final sample size refers to the whole bucket (orange + green try visitors), one of them (orange visitors) or clicks sizes (orange + green clicks?).
What is 4791 referring to?
4791 would refer to the total number of samples, so in this case, the total number of visitors exposed to the experiment.